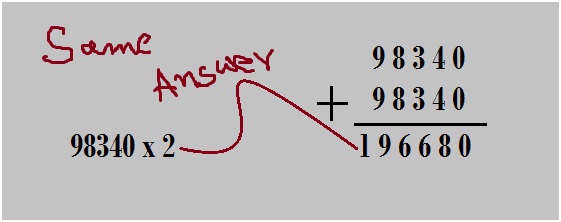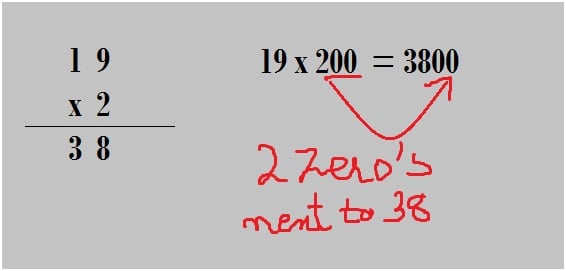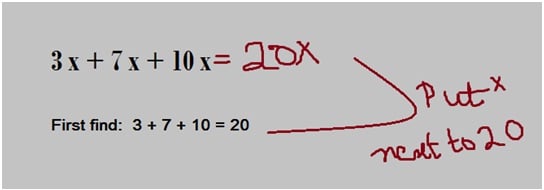Tag Archives: chat with a Live Math Tutor Online

Learning Math without Anxiety is Possible through Online Tutor

Posted on by
2

best online Math tutor

Math is essentially a brain twister and it often tests a student’s patience to the core. Once you do not get a right answer in your homework sum or exam question, you feel like being drawn to the end of the world and manage somehow to come out of the situation. In the case of many students, they start feeling allergic to Math and try to shun Math classes thereafter.

How mental blocks in Math learning are developed?

Students dread Math thinking it is the acquisition of a few gifted Math brains. Actually,  anxiety, fear and  phobia developed by Math myths  turn to be mental blocks in course of time obstructing students from learning Math with confidence. Further, negative happenings in the past Math classes and discouragement from parents and peers lead to the formation of negative feelings and lack of self confidence in students while attempting Math problems.
Top 5 Reasons Why An Online Math Tutor Is Your Key To Scoring Straight A

Who can save you from mental blocks in Math learning?

Personal orientation through positive thinking can be an option for removing mental blocks in Math learning. Or friends and peers can help a student come out of his negative thinking about his Math abilities through suggestions and friendly talk. Above all, a virtual Math tutor can be the best sort in this context with his patient approach and personalized techniques. There too, the best online Math tutor does his part very well in removing the mental blocks of a student through his diagnosis test, one on one tutoring sessions and custom made approaches.

Once a student gets relieved of his mental blocks, his natural abilities rush to the front and he is able to ace Math just like that. He feels happy with his Math skills and gets ahead with a positive thinking about his Math classes and participates in them with interest.

Thus, Math online tutoring is the easiest way to get rid of mental blocks for successful Math scores.

10 Useful Lessons You Will Learn During High School

Posted on by
Reply

High school is a critical learning phase in education. You develop into a fully fledged independent learner during this tenure and go beyond mere comprehension of topics to analyze the matter and understand the world around you.

10 Useful Lessons You Will Learn During High School

Here are 10 valuable lessons you learn through high school education.

1. Importance of attendance

Making your presence in the class is the great part of the game. It also constitutes a good percentage of your grades. When it develops into a habit, your presence in the work place makes significant difference in your performance and helps you in winning promotions and bonus and making your contributions in the work areas worthy and notable.

2. Being punctual

More than being present, it is better to be punctual. Anyone who is punctual is acclaimed high and a person who comes late becomes an object of observation for teachers and students. It is good to give up tardiness and make punctuality as one of your essential values.

3. Putting in hard work

Hard work always pays off in your presentations, assignments or homework. Just skimming through night studies or superficial learning of the subject matter will not fetch fineness and perfection in your school work and as a high school student you will not win the grades aspired by you. Put your heart and soul in whatever you do and you can get the best for it. Seeking outside help like online tutoring, referring to grading guides for extra edge are skills you develop during high school years. This will continue through your life and career for success.

4. Socializing is important

High school offers lots of opportunities for socializing and there need not be any limit for keeping friends with your peers or others and can be intimate with them as well. It develops confidence and understanding of the world around you. Participate in social, academic and sports clubs as much as possible and make the most of your socializing.

5. Know your attitudes and aptitudes

While learning in high school you can have an understanding of what you are passionate about and what goals you want to achieve in academics and other areas. You can estimate what job you want to pursue and how you would go ahead with it. You have an opportunity to know about yourself without simply following the examples of others.

6. Be on good terms with teacher

Teachers are your guides and you need to be in their good books for getting right directions from them. When you are continuously keeping in touch with them, they understand that you value their time and try to see things in your way. Be attentive in the class, participate and ask questions. Attend office hours. All these help you make a good impression about you upon the teachers. This comes a great way when you pursue a career where your employer gets impressed by you at the very first sight.

7. Understand what kind of learner you are

Learning styles differ and you need to know what kind of learner you are. Experiment with various learning styles and find out which one comes naturally to you. Learning at your pace and style helps you comprehend the subjects well and go more than that to explore the subjects. This also helps you in your work place with critical thinking abilities and ability to navigate information.

8. Study in company

Studying with a buddy helps you greatly in getting constructive criticisms while rehearsing for a presentation or debate or oral exams. You get different insights about topics as well. Further, it is good cheers to make company and enjoy learning as a joyous process.

9. Working in groups

Team work is the essence of today’s work scenario in any career. Working in groups at high school level for a project, discussion or debate definitely brings forth good team spirit, co ordination, empathetic values in you. It even can develop a patient approach towards others and things. Lots of opportunities are available for you to pick up team work in high school which shapes your future requisite in advance.

Read more – How to eliminate high school math tension through homeschooling

10. Thinking critically

You are starting your journey into adult world by the time you reach high school. Now, it is time for you to understand and judge the world around you. It is not simple understanding of the subject that is expected of you but you need to go beyond that to critically examine what you learn. This critical thinking ability comes a great way in your future assignments in college and career.

Conclusion

Thus, high school learning is crucial promoting good opportunities in you to learn valuable lessons for life, future studies and career. Make use of the precious time during this phase and cultivate life skills that come a long way in your life.

9 Must Know Methods for Solving Math Problems

Posted on by
2

Math has many topics and there are various kinds of questions related to each given topic. To solve a given math problem different kinds of methods and formulas can be used. Today, we will try to learn and understand 9 most basic and useful methods utilized while solving Math questions. Let us get started:

1. Method for calculating the LCM (Least Common Multiple)

Finding the least common multiple for the given numbers. I am pretty sure most of you have observed that LCM are part of problem solving for no matter which math topic you are working on. We need to calculate the LCM’s in simple topics like fractions, decimals and they may be also required to be calculated while solving questions in algebra, geometry and many more. Follow the example below:

What is the LCM of the two numbers 6 and 15?

For finding the LCM (least common multiple) first write the multiples for the given numbers.

Remember the 6 times table? Yes! They are all the multiples of number 6, so you have 6, 12, 18, 24, 30…. .

Now the 15 times table, don’t worry you need to check only till you get the common multiple.

So you have 15, 30, 45……………..

Did it strike a bell? Well look below for more clarity:

LCM

Hence the LCM for 6 and 15 equals to 30. (Sometime there can be more than one common multiple, always pick the least number as the LCM.)

2. Method for calculating the GCF (Greatest Common Factor)

Following the LCM is another interesting method in number theory. You guessed it right! The GCF (The greatest common factor.) For finding the GCF the Tree diagram method is very common. Here is a question: Find the GCF for the numbers 21 and 35? The first step is to write the tree diagram for 21 and 35. Try to follow the tree diagram below: GCF Using this tree method, you will get 21 = 3 x 7 and 35 = 5 x 7. (Note: 1 is always a factor for any given number.) Here 7 is the common factor for 21 and 35, which can be written once as its repeating in both the numbers. The Greatest common factor includes the remaining factors from both the numbers as well. Do not forget to include the 5 and 7. Hence GCF for 21 and 35 equals 3 x 5 x 7 = 105. After the LCM and the GCF, let us look at the method for changing the decimal numbers into fractions. Follow the example carefully:

3. Method of converting the decimal numbers into fractions

Convert the given decimal number 0.3 into a fraction. Here given to us is a decimal number. Count the number of decimal places. The number 0.3 has only one decimal place. Now while changing into a fraction multiply the numerator and the denominator by 10 for every decimal place. Here, since there is only one decimal place multiply by 10. Try to follow the diagrams below: decimal numbers into fractions Hence 0.3 can also be written as 3/10.

4. Method for solving Unit and Total Price word problems

Time to solve a work problem on price and money:

Anna and Ben went to a park. Anna brought 3 balloons and Ben brought 2 balloons. Find the total amount of money spent if each balloon costs $0.25.

For the given question you need to first calculate the total number of balloons Anna and Ben brought = 2+ 3 = 5.

Now comes the crucial point the decimal multiplication. Each balloon costs $0.25, so 5 balloons costs 5 x 0.25. Need help? Look at the diagram below:

Total Price

Hence the total price spent by Anna and Ben = $ 0.75.

Well problem solving is incomplete without equations. The next few methods will help you solve equations.

5. Method for solving one step equation using Addition

Find the value of y in the equation y – 6 = 12?

In the given equation 6 is subtracted from y. So the reciprocal operation needs to be applied to the equation. Add 6 on both sides of the given equation. This gives:

one step equation using Addition

Hence, the value of y = 18.

6. Method for solving one step equation using Subtraction.

Find the value of x in the equation x + 30 = 150? In the given equation 30 is added to x. So the reciprocal operation needs to be applied to the equation. Subtract 30 on both sides of the given equation. This gives: equation using Subtraction Hence the value of x = 120.

7. Method for solving one step equation using Multiplication

Find the value of y in the equation y/2 = 7? In the given equation y is divided by 2. So the reciprocal operation needs to be applied to the equation. Multiply by 2 on both sides of the given equation. This gives: equation using Multiplication Hence the value of y = 14.

8. Method for solving one step equation using Division

Find the value of x in the equation 5x = 45.

The given question has the equation with one variable x. I believe, by now did you get a hold of this method? The reciprocal operation of multiplication is division. Divide both sides of the equation by 5. This gives:

equation using Division

Hence the answer to the given equation is x = 9.

9. Method for solving Expressions using substitution

Now, what if there is an expression with more than one variables and you need to find the value of the expression. Here is what needs to be done:

Evaluate the value for the expression 4x – y, when x = 1 and y = 2.

Here for this question the method of substitution can be applied. You are given the value of x = 1 and y = 2. Hence substitute the values in the given equation to solve the question.

Not really sure how! Try to follow the diagram below:

Expressions using substitution

Much better, isn’t it! So after substitution here is how the expression will look like: 4(1) – 2 = 4 – 2 = 2. Hence the solution = 2.

We are not done yet! These were just few methods to get you started on solving math problems. To know more chat with a live Math tutor online and get more interesting details about the topic.

chat-now

9 Secrets To Know About Speed And Mental Math Tricks And Techniques

Posted on by
2

Math is definitely challenging but what makes learning math fun and interesting is that, there are some tricks and techniques which can actually make the calculations easy to solve. Today, we will try to learn some math tricks which can be applied in solving different kinds of questions.

Speed And Mental Math Tricks

Multiplying a given number by 2

We all know the 2 times table. But what if 2 is being multiplied to a bigger number, there is a trick to make the multiplication quick and accurate. Think about it, multiplying by 2 it is nothing but doubling the given quantity. So to speed the calculations the given number can be added twice instead of multiplying by 2. For example 6 x 2 = 12.

This can also be got by 6 + 6 = 12. Now, if there is 32 x 2 = 64. This can also be got by 32 + 32 = 64.

Now applying this trick to bigger numbers multiplied by 2.

Find the value of 98340 x 2?

One method is the usual way of multiplying the given number by 2. But let us solve the same question with the trick of addition:

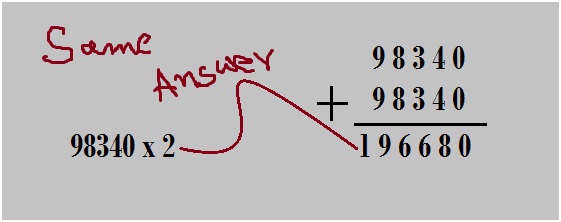
math 1

Hence 98340 x 2 = 1,96,680

Multiplying numbers which are multiples of 10

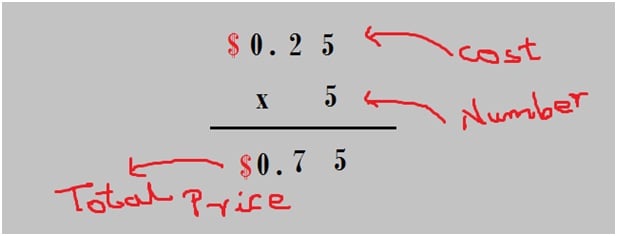
Did you know 10 is a very interesting number when it comes to multiplication? For example, in a question you come across a calculation such as 23 x 10 all you need to do is place a one zero next to 23. That is 23 x 10 = 230.

Can this be applied to bigger numbers as well? Yes it can! Let us look at some more examples:

While multiplying, 45 and 50 one method would be the regular multiplication. By applying the trick here all that needs to be done is 45 x 50, first find the value of 45 x 5 = 225. Since there is 50 which is a multiple of 10 place a zero next to 225.

So we get 45 x 50 = 2250. Another example would be, 25 x 30. Here first do 25 x 3 = 75. Now since there is 30 place a zero next to 75. This gives 25 x 30 = 750

Question: Sam brought 19 boxes of candies. Each box contains 200 candy bars, find the total number of candy bars in all the boxes.

Number of boxes of candies Sam brought is 19. Each box contains 200 candy bars.

Hence the total number of candy bars equal = 19 x 200.

Try to follow the diagram below for the calculation:

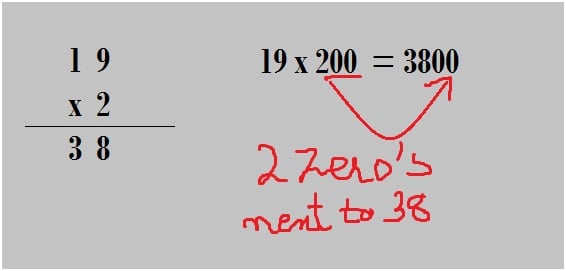
math 2

Multiplying a given number by 11

No matter what number is given to you multiplication with 11 can become quite simple, follow the trick here. Look at eleven, there are two 1’s. Now for example you have 14 x 11. First do 14 x 1 = 14 then to this add 140 which is 14 + 140 = 154?

So we get 14 x 11 = 154

Need a better idea? Follow the example below:

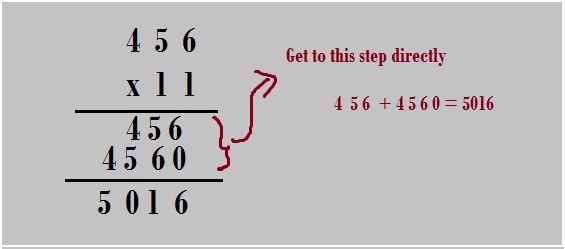
Find the value of 456 x 11?

Here first calculate 456 x 1 = 456 now add 4560 to it so you get 4560 + 456 = 5016

math 3

Adding three or more digit numbers

In some questions, you may have had situations where more than 2 numbers need to be added, it can get more tedious if they are big numbers. Let me share a little secret that can make adding such numbers much easier. For example there is a word problem: Riya spent $ 112 on shoes, $ 216 on bag and $315 on books. Find the total amount of money Riya spent on all the items. Solution: For the given question, the total amount of money spent equals the sum of all the given individual prices = $ 112 + $ 216 + $ 315. Follow the trick here, rather than adding the individual number. Add the hundreds place first. Follow the solution: math 4

Squaring number ending in 5

This rule is applicable from 5 to 95 only (i.e., 5, 15, 25, 35, 45, 55, 65, 75, 65, 75, 85, 95.) and here is how it works! We have 5 x 5 = 25.

The trick is, for a number ending in 5 when squared always has to end in 25. So for a given number example 152 pick the tens place, which is 1. Now the number after 1 is 2. Multiply 1 x 2 = 2. Now place a 25 next to 2. We get 225.

Now for 25 x 25. Here, 2 is in the tens place. What is the number next to 2, 3. So do 2 x 3 = 6. Now place a 25 next to 6. We get, 25 x 25 = 625.

Let us follow the diagram for clarity, take 65 x 65.

math 5

Hence 65 x 65 = 4225

Divisibility rule for number 2

Here is a quick mental math trick to find weather a given number is divisible by 2 or not just by looking at it. If a number is ending with an even number then it is divisible by 2.

What are all the even numbers between 0 and 9 (0, 2, 4, 6, and 8).

Look at an example: 48 here 8 is an even number so it is divisible by 2. Now 51 is not divisible by 2 as 1 is an odd number. Apply the same for big numbers.

Find out if 4576 is divisible by 2? Prove it!

Here 4576 is ending with number 6. Since 6 is an even number the given number is divisible by 2. Follow the diagram for a quick check:

math 6

Divisibility rule for number 4

Now that you are familiar with the divisibility rule for 2. Let us quickly check the divisibility rule for number 4. When it comes to 4 always check whether the last 2 numbers are divisible by 4. Consider 324 here it’s clearly know that 24 is divisible by 4 so 324 will be divisible by 4. Now let me give you another example:

Find out whether 5608 is divisible by 4? Check your answer.

Here again use the trick and figure it your mind. 08 are the last two numbers of the given number. Since 08 is divisible by 4, 5608 is divisible by 4. Let’s check if we got it right look at the diagram below:

math 7

Divisibility rule for number 5

Did your math calculations get faster on the divisibility part? Now let us follow the trick for checking divisibility with number 5. For number 5, the given number should end either with 0 or 5. Take an example of 560 it is divisible by 5 since its ending in 0. Whereas 432 is not divisible by 5 since its ending with 2 not 0 or 5. Look at the following question.

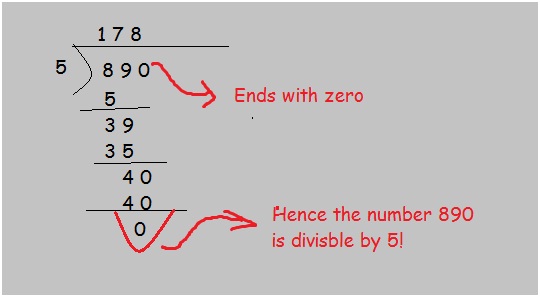
Find out if 890 is divisible by 5? Check your answer.

Here the given number 890 is ending in 0, so it is divisible by 5. Let us check the answer, follow the diagram below:

math 8

Combining the like terms

Many students find adding and subtracting like terms very confusing. Let us look at a simple way of solving this kind of a question. Did you know there is a trick with which you can solve the combining like terms in your mind? Here is what can be done:

Consider a question for finding 5x + 6x.

A like term is a term which have the same variable. Here it is x. Now for adding 5x and 6x since x is the same, just find 5 + 6 = 11. Hence 5x + 6x = 11x.

Did you follow the solution? Follow the next example:

Find the value of 3x + 7x + 10x?

All that needs to be done is add the numbers and place the common variable x next to the sum. Take a look at the diagram below:

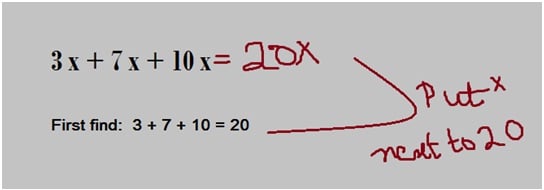
math 9

Hence the solution is 20x.

Therefore, practice these tricks and apply them in your math calculations. You will be amazed how they will aid in speeding your calculations. If you still need help, chat with a Live Math Tutor Online Now!