Logarithms are really fun and interesting, but I have seen many students find changing logarithmic notation to exponential notation and vice versa quite confusing. Well here are some useful tips to make you remember that this conversion is simpler than you have expected.
The exponential form is where we have the base number multiplied according the exponent to get the answer. Here is an example from online math tutor:
When you multiply 2 four times you get 16. That is 2 x 2 x 2 x 2 = 16.
This can be written in the exponential form as 24 = 16. Let’s look deeper into this notation:
Let’s now try to follow how we can convert the exponential notation to the logarithmic notation:
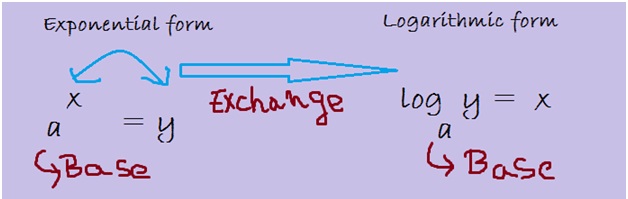
As show above, both the exponential notation and the logarithmic notation have the same base number. Next, there is an exchange in the exponent and answer while writing it in the logarithmic notation.
How to Solve #Algebra Word Problems in 5 Steps http://t.co/kg6CqctO6O #backtoschool #homeschooling pic.twitter.com/wApx3S0D5R
— Tutor Pace (@TutorPace) August 4, 2015
This can be better understood with an example:
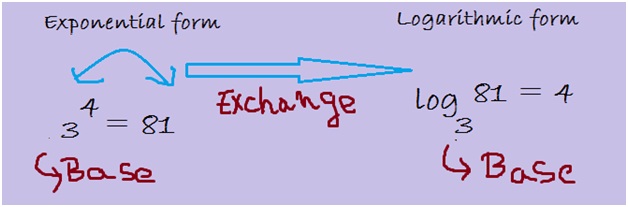
Convert 34 = 81 from an exponential notation to logarithmic notation.
Here 3 is the base number which will remain the same even in the logarithmic form.
We have 4 as the exponent and 81is the answer which can be written as:
Did you get a little hold of this method? Good let me show you one more example:
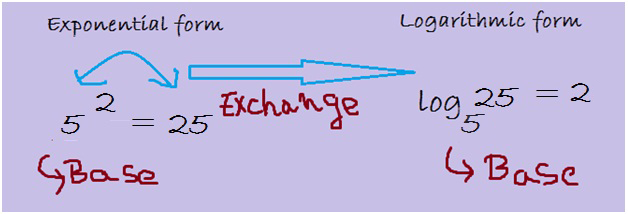
Convert 52 = 25 from exponential form to logarithmic form.
Everyone likes the 5 times table, for some reason it’s quite easy to memorize.
Here observe 5 is the base number and 2 happens to be the exponent. Multiplying 5 x 5 gives 25 as the answer. Now converting the exponential form to logarithmic form:
Taking a step further, let us now convert the logarithmic notation into exponential notation applying the same process backwards.
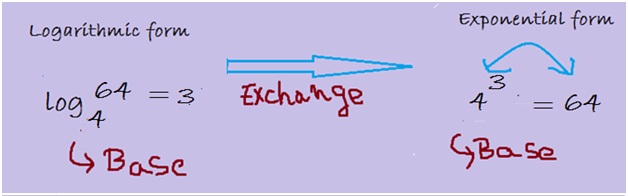
Convert log4 64 = 3 from logarithmic notation to exponential notation.
Here the given logarithmic notation can be changed to exponential notation by keeping the base number 4 the same. Follow the steps below:
Hence the exponential notation for the given question is 43 = 64.
How To Sort And Solve Elapsed Time Story Problems http://t.co/j3zGC5Q6m8 #algebra #backtoschool #homeschool pic.twitter.com/dzdb9M73Rl
— Tutor Pace (@TutorPace) August 4, 2015
Good so far! Now, have you ever observed some logarithms written without a base?
For example, notations like log 5, log 16 or log 150. Are they really without any base number? The answer is NO! They have a base number which is 10 it’s called the common base.
Hence, logarithms with base number 10 are called common logarithms. This can be shown as below:
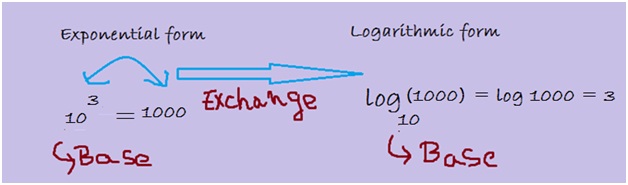
Convert the given exponential form 103 = 1000 to logarithmic form?
Here we have the base number for the exponential form as 10, so the final answer will be a common logarithm. Hence we can write the given question into a logarithmic notation as follows:
So the final answer is log (1000) = 3. [Not to forget it still has a base 10.]
100 #LessonPlans And Ideas For Teaching #Math http://t.co/gWy2T5eKsT
— Tutor Pace (@TutorPace) August 3, 2015
Now you are familiar with the logarithmic notation and ready to change exponential notation into logarithmic notation. But remember logarithms does not stop here, these are just few useful tips to get you started with the logarithmic notation.
Read more – Solving Logarithmic Equations


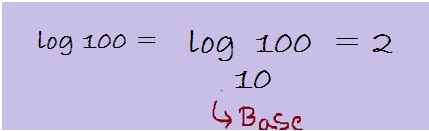

One of your examples (in a mauve box) shows, on the left, 5 squared = 25, then on the right, log2 of 25 = 5. This is wrong. You should write, log5 of 25 is 2.
Hello Charlis,
Thank you for pointing the errors. I have gone and corrected it.
Again thanks
Have a good one….