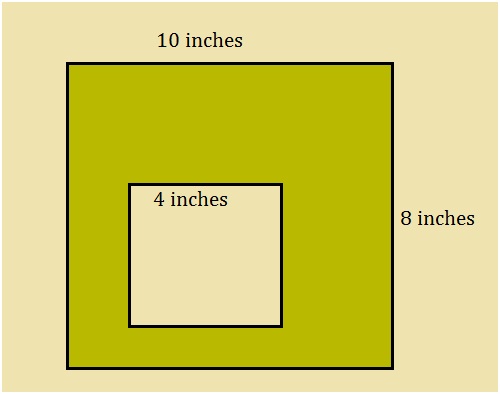
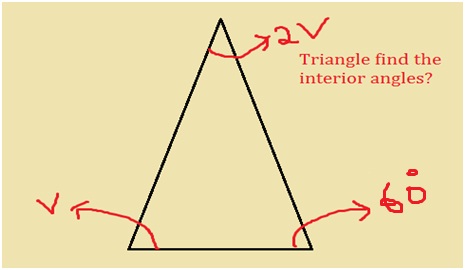
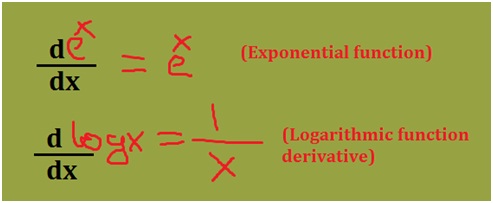
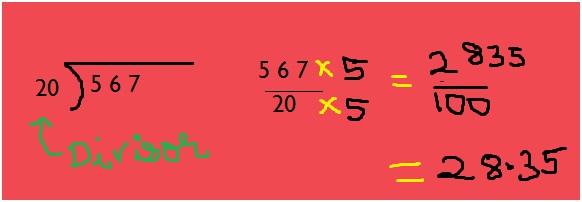
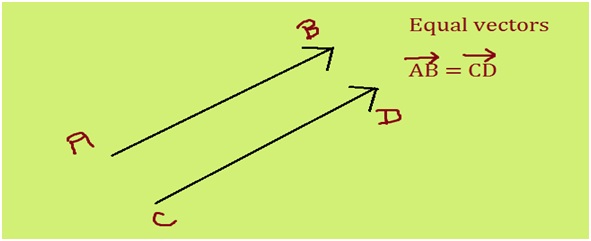
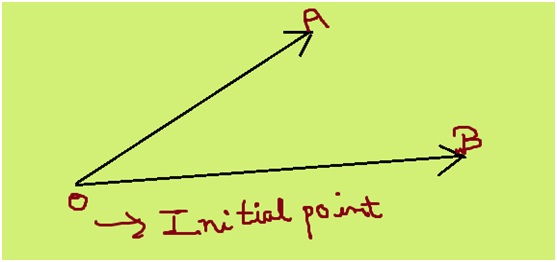
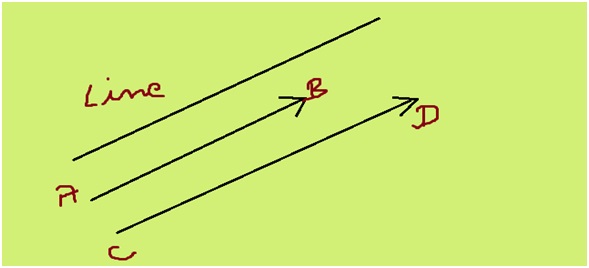
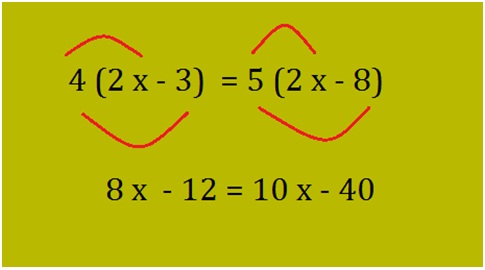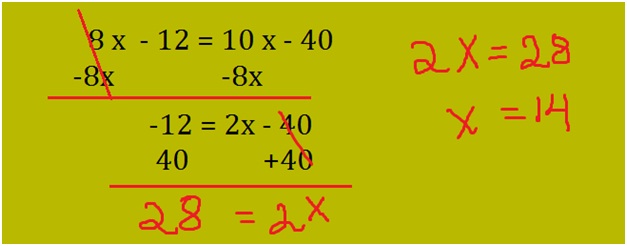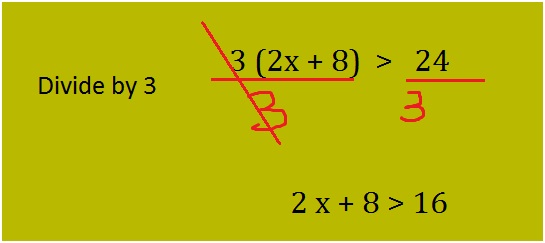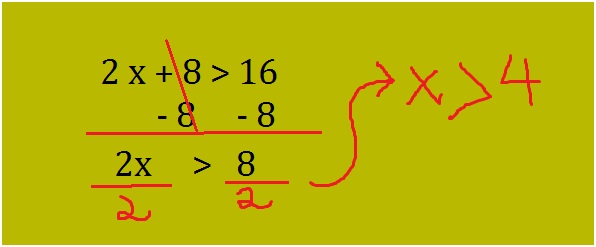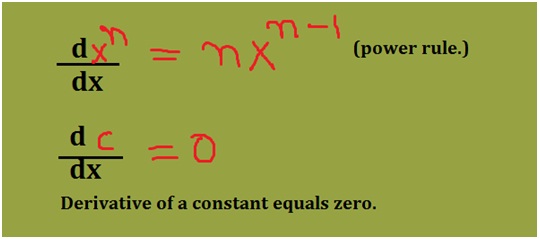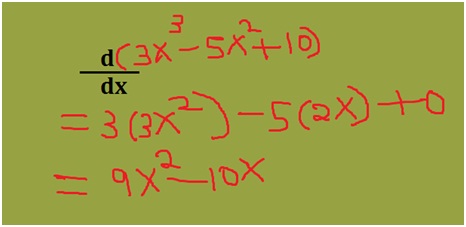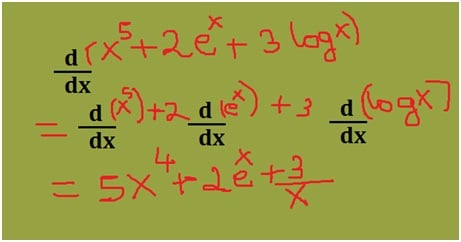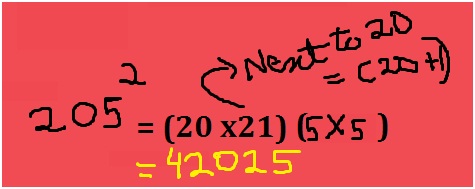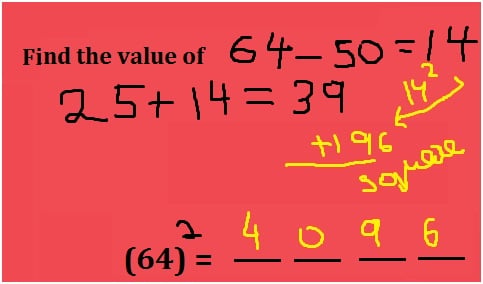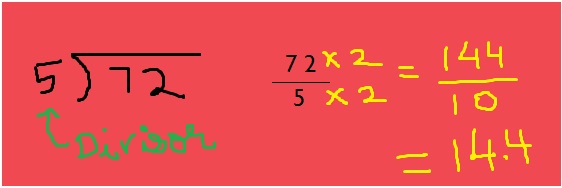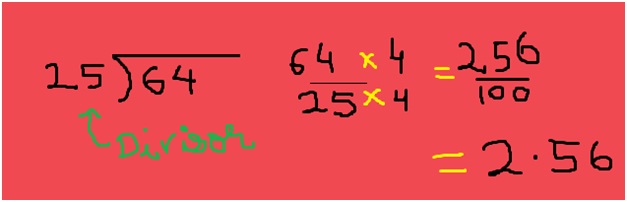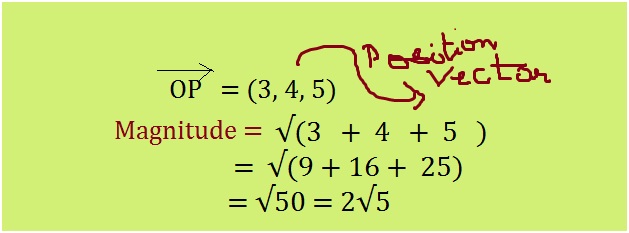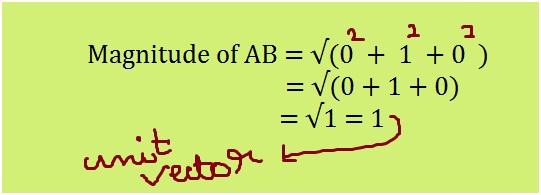Tag Archives: Free Online Math tutor

7 Tips for Finding the Right Online Math Tutor

Posted on by
3

How do you know your child needs math assignment help? Some of the more obvious signs are falling math grades on your child’s report card or on individual math assignments. A change in attitude toward math can also indicate difficulties. If your child loved math last year, but suddenly dislikes it, he or she could be experiencing difficulty mastering new math concepts.


Math difficulties can arise at any stage of the learning process.

Working with a math tutor, including an online math tutor, should be explored as soon as you realize your child is having difficulties. Throughout school, math lessons build on what was taught before, and failing to master a single concept can result in multiple math difficulties later on. Once you make the decision to work with an online math tutor, how can you be confident you have found the right one for your child? Here are 7 tips for finding the online math tutor that will benefit your child most.

1. Look for a Tutor Who Specializes in Math

Even if your child is in elementary school, it’s worthwhile to look for an online math tutor who specializes in math. While there are general tutors who can offer math assignment help, a tutor specializing in math is more likely to have the depth of knowledge necessary to understand the specific concepts that hold children back and how to address them.

2. Find a Tutor Whose Schedule Works With Your Child’s

The great thing about the internet is it never closes, and you can interact with someone on the other side of the world if you want. That said, it’s important to find a tutor who will be available during the hours your child works on math. If you’re considering an online math tutor from several time zones away, ensure his or her schedule meshes with your child’s before committing.

3. Choose a Tutor Willing to Work Interactively on Concepts

Math assignment help should be interactive. A good online tutor doesn’t simply lecture or present concepts, but interacts with students: “What do you think the first step should be?” Your child’s tutor should be able to develop a working rapport with your child, striving to understand his or her questions and difficulties so as to address them most effectively.

4. Look for a Tutor Willing to Explore How Not to Solve Problems

Sometimes a child needs to be shown how or why what might seem to be a solution doesn’t actually work. A great online math tutor understands how something might intuitively look right, yet not be. There may be occasions when a tutor needs to go through the wrong procedure with your child to show where and why problems occur.

5. Select an Online Tutor Who Uses Plenty of Visual Aids


Online math tutors should have easy access to helpful visual aids.

Diagrams, pictures, animations, and other visual aids can be tremendously helpful. For example, a child having difficulty with fractions may have an easier time if concepts are demonstrated through something he is familiar with, like LEGO. Try to choose a tutor who knows where to look online to find GIFs and other visual aids that help explain mathematical concepts.

6. Pick a Tutor Who Knows How to Assign Subject Matter in Context

Some children, for example, have no trouble applying concepts like basic arithmetic operations, but have trouble knowing which one to apply in word problems. Other children may not be motivated to perform an arithmetic operation without some sort of context (like a story problem) in which it makes sense. Your online math tutor should take time to learn how your child learns.

7. Try to Find a Tutor Who Is Open to Feedback

You don’t want an online math tutor who is resistant to feedback. After all, the goal is to help your child master important concepts. Knowing what works well and what doesn’t is important for an online math tutor in order to provide the best possible service. Discuss feedback before hiring an online math tutor to ensure the one you choose is open to suggestions and discussion.

In Conclusion

Hiring an online math tutor is an option many parents didn’t have when they were learning mathematics, and it can make a world of difference in your child’s ability to master mathematical concepts and keep up with what is expected of him or her. Know what to look for in an online math tutor, and you can be confident that when your child needs math assignment help, he or she will have access to someone who understands math, understands your child, and is willing to work with your child’s learning style. Are you interested in hiring an online math tutor for your child? Tutor Pace can help, and we encourage you to get in touch with us at your convenience.

Math For Advanced Level; Algebra Geometry And Calculus Advanced

Posted on by
Reply

mathclass

Math is a combination of many branches such as Algebra, Geometry and Calculus, but math does not quite stop right there, we have levels to each branch of math such as beginners and advanced. The advanced level math usually needs more attention and practice to master it. If you are confident with the basics and know all your formulas then the advanced level math is the next step to beginner math topics. Today let us look at different advanced level math questions in areas such as Algebra, Geometry and Calculus.

Advanced level Algebra

Algebra consists of different algebraic expressions and equations. Algebra has different kind of questions to solve. Mentioned below are few such questions which will give you an idea about how to use the basics of algebra to solve advanced level questions:

Solving linear equations with one variable:

Find the value for x in equation 4 (2x – 3) = 5 (2x – 8)?

Here the unknown variable is x. Since there are numbers in front of the brackets, distribute the numbers as shown below:

math1

Here we have x on both sides of the equation, bring all like terms to the same side of the equation and solve for x.

math2

As show above the equation reduces to 2x = 28. Divide by 2 on both sides of the given equation. This gives x = 14.

Did you follow the solution to the question above? Now let us look at solving an inequality. Solving inequities play an important role in algebra. An inequality is where there is a comparison and is represented by a less than or greater than symbol. The solution to the inequality are usually represented on a number line, so as to represent all the possible values for the variable. Follow the given example below:

Solve the given inequality 3 (2 x + 8) > 24?

Look at the question we have greater than symbol here. You have to solve for the unknown variable x and find all the possible solutions for it. For the given question above, divide both sides of the equation by 3 as show below:

math3

Now the inequality is reduced to the form 2x + 8 > 16. The next step is to solve for x. follow the steps below:

math4

The inequality is now reduced to x > 4. Look at the symbol separating x and 4 it’s a greater than sign not greater than equal to. This implies that the number 4 is not included in the solution. Hence the solution of x contains all the values greater than 4 such as 5, 6, 7, 8…….. This can be represented on a number line as show below:

math5

The advanced level algebra consists of many other subtopics such as quadratic equations, solving two variable equations using substitution and elimination methods and many more. The key to success for solving all such questions is practice and knowing the basics of Algebra.

Advanced level geometry:

After algebra let us look into geometry and some sample question. Geometry is one of the favorite topic for all the students especially when you are in the elementary school, it could be because of learning different kinds of shapes. But geometry does not quite stop there, as you go to the higher grades you need to tackle the advanced level. Let us look at two examples on how the basics of geometry can be helpful to solve the advanced level geometry question.

 Find the area between the two shapes for the given geometric figure:

math6

The given diagram is a square inscribed in a rectangle. Let us recall the formula for the area of the rectangle = length x width. Using the formula, the area of the rectangle = 10 x 8 = 80 square inches.

Now the area of the square = side x side. Using the formula, the area of the inner square = 4inches x 4inches = 16 square inches.

The area between the two geometric figures is obtained by the difference in the areas.

Hence, the area = (80 – 16) square inches = 64 square inches.

Did you follow the solution? Great! The next question you will see how the sum of the angles can be used to find the missing angles of the triangle.

The sum of all interior angles of a triangle = 180 degrees. This fact is very commonly used in solving many geometrical questions. Knowing the angle measures helps you classify the different kinds of triangles such as equilateral, scalene, and isosceles.

In the given diagram, find the value of v and the angles of the triangle. Classify the triangle?

math7

Sum of all the angles of a triangle = 180 degrees.

Adding all the angles of the triangle v + 2v + 60 = 180. This gives 3v + 60 = 180.

Solve for the variable v, follow the steps below:

math8

The angles of the triangle are v = 40 degrees, 2v = 2 (40) = 80 degrees and the third angle is 60 degrees. Therefore, the angles of the triangle are 40, 60 and 80 degrees. Since all the angles of the triangle are different. The given triangle is a scalene triangle.

Advanced level Calculus

The next branch of mathematics which is very important and plays a major role in high school and college level math is calculus. The students are expected to know pre-calculus before stepping into calculus or advanced calculus. Calculus starts off form the basics of functions, domain, range and steps into differentiation and integration, which are the advanced level topics.

Let us take a quick look at few solved calculus questions:

Find the derivative to the function f (x) = 3x3 – 5x2 + 10?

Here before finding the derivative of the given question there are some formulas of derivatives which are expected to be known. Learn from the diagram below:

math9

Did you recall the formulas? Now apply the power rule to 3x3 and -5x2. Since 10 is a constant the derivative will be zero. Take a look at the diagram below:

math10

The answer f’(x) = 9x2-10x.

Taking a step forward, let us solve a derivative question involving logarithms and exponential functions.

Find the derivative of the function f(x) = x5 + 2ex + 3log x?

For the given question you can apply the power rule to x5, exponential rule for 2 ex and logarithmic rule for 3 log x. Use the formulas as mentioned in the diagram below:

math11

Applying the formulas to the given function:

math12

Hence the solution f’(x) = 5x4 + 2ex + 3/x.

Free Online Math tutor is the easiest way to get solutions for difficult Math problems. Tutor Pace provides effective Math tutoring and assignment help which are personalized and customized to meet student demands in one to one sessions.

5 Vedic Math Secrets for Every Student to be a Math Genius

Posted on by
4

Did you ever hear about Vedic Math and wonder what exactly is it? Vedic Math is derived from the ancient Indian scriptures called as the Vedas. The Vedic math is very ancient and it has many interesting tricks and facts which can help improve a student’s ability to solve the given question. We will look through some Vedic math secrets that you can apply in your math problem solving. This should make you not only solve the questions faster but also very efficiently.

Vedic Math Tutor

Here are some methods:

1. Squaring of a number ending in 5.

Find the value of 352?

The number ends in 5 the square of it should always ends with 25. In front of 25 place 3 x 4 = 12. That is the product of 3 and its consecutive number which is 4. Follow the diagram for a better idea:

math 1

Did you follow the trick? The more you practice, you will be able to solve these questions in one step. Now let us look at the longer version for the same question:

math 2We get the same answer!

Take a look at one more example to master the skill.

Find the value of 952?

Here since the number is ending is 5, the square will end in 25. In front of 25 place the product of 9 and 10. Follow the diagram to apply the method:

math 3

The answer is 9025.

This can be applied to three digit numbers as well. But the point to note is the number should end in digit 5.

Find the value of 2052?

The number ends in 5, so the square of the number will end in 25. For the next step follow the diagram below:

math 4The answer for the three digit multiplication for 205 x 205 = 42025. Check the answer in the longer method as well you will get the same value. 2. Square of numbers between 30 to 70? In this method we can find the square of the number between 30 and 70 within no time. Usually it takes us the regular multiplication method or the calculator to find the square of a number. Imagine, if you can solve it in the mind in a fraction of few seconds. Find the value of (51)2? Step 1: Find the difference between the given number and 50. You get 51 – 50 = 1. Step 2: Now add the difference to 25, this gives 25 + 1 = 26. (These are the first two digits.) Step 3: The last two digits of the square will be equal to the square of the difference.

Follow the diagram for the next step:

math 5

Find the value of (64)2?

Step 1: The difference between the given number and 50. You get 64 – 50 = 14. (As 64 > 50)

Step 2: Now add the number 14 to 25, this gives 25 + 14 = 39.

Step 3: Calculate the square of the difference 142 = 196.

For the last step follow the diagram.

math 6

Find the value of (44)2?

Step 1: The difference between 50 and 44. You get 50 – 44 = 6. (As 44 < 50)

Step 2: Now subtract the number 6 from 25, this gives 25 – 6 = 19. (First 2 digits of the square.)

Step 3: Calculate the square of the difference 62 = 36. (Last 2 digits of the square.)

For the last step follow the diagram.

math 7Hence the number is 442 = 1936. (Practice this method for more numbers.)

3. Subtracting any given number from 1000.

In this method for the given number that has to be subtracted from 1000, subtract the ones place by 10 and the remaining numbers by 9. For a better idea try to follow the examples shown below:

Find the value of 1000 – 356?

For this question subtracting 6 from 10 and 3, 5 from 9. Follow the diagram below:

math 8

Hence 1000 – 356 = 754.

Once you get a hold of this method you will be able to subtract quickly in your mind. This can also be applied to numbers when subtracted from 10 or multiples of 10, such as 100, 1000. 10000 and so on.

Let us take a look at another examples:

Find the value of 10000 – 8943?

Here subtract the digits in 8943 such that, ones place is subtracted from 10 and the remaining numbers from 9. Follow the diagram:

math 9

Hence the answer to 10000 – 8943 = 1057.

4. Finding the cube root of a given number.

In this method you will be able to find the cube root of any given number within a fraction of few seconds. You need the values of cubes from 1 to 9 for finding the cube roots. Here is the list:

math 10

The number 2744 has a cube root. Find the cube root 2744?

For this method you need a confirmation that 2744 has a cube root. Once you are sure of it, check the last number which is 4. Which cube in the list has the last number 4? 43 = 64. Now cross of the last three numbers and follow the diagram below:

math 11

The number 593919 is a cube of a number. Find the cube root of the number?

Here the given number is ending with 9, so the last digit of the cube roots should be 9. Since 93 = 729. For the next steps follow the diagram below:

math 12

As observed in the diagram above after crossing the last three numbers 59 is closest to 27 which is 33. Hence, the cubic root is 39.

5. Division of numbers made simple.

Find the value of 72 divided by 5?

Here the number 72 is divided by 5. Observe the number 5 can be written as 5 x 2 = 10.

The solution can be found easily within no time as follows:

math 13

Find the value of 64 divided by 25?

Here the number 64 is divided by 25. Observe the number 25 can be written as 25 x 4 = 100.

Follow the diagram below to get the solution:

math 14

Hence the value for 64/25 = 2.56.

This can be applied to bigger numbers as well such as:

Find the value of 567 divided by 20?

Here as well take a look at the divisor which can be written as 20 x 5 = 100.

The next step is to multiply the numerator and denominator of 567/20 by 5.

math 15

Hence the solution for 567/20 = 28.35.

Did you observe math calculations which usually take many steps to solve can be calculated in the fractions of few seconds? Well there are many more math secrets which can make using the calculator optional. So keep learning and engage yourself in discovering many more tricks. All the Best!

Free Online Math tutor is the easiest way to get solutions for difficult Math problems. Tutor Pace provides effective Math tutoring and assignment help which are personalized and customized to meet student demands in one to one sessions.

Linear Algebra Math Made Simple: The Study Of Spaces

Posted on by
Reply

Today we will be looking at the basic concepts and properties of linear algebra. Linear algebra can also be called as vector algebra, as it is the study of vector spaces. You may now wonder what exactly vectors are. Well, quantities are classified into two types such as scalars and vectors. A scalar quantity is a quantity which has only magnitude and no direction. A quantity which has both magnitude and direction is called as a vector.

Girl doing homework

Let us look at some definitions and properties of vectors which will make the study of the vector spaces much simpler.

Position Vector: The position vector locates any given point in the three dimensional rectangular coordinate system. Let us recollect that the three dimensional rectangular coordinate plane has x, y and z axes. The origin point for such coordinate system is given by (0,0,0). The position vector or any point P in space is given by OP (x, y, z). The magnitude of the vector |OP| can be given by √(x2 + y2 + z2).

So, we have |OP| = √(x2 + y2 + z2).

Let us take a look at one of such example question.

Question: What is the position vector of the point (3, 4, 5). Find the magnitude of the given position vector?

The position vector is found from origin (0, 0, 0) to the point P. Follow the steps in the diagram below for finding the magnitude of the given vector:

math 1

Let us now take a look at some basic types of vector spaces.

Null vector: A null vector is also called as the zero vector. Remember the starting point of the vector is called the initial point and the ending point is called as the terminal point. The vector for which both the initial point and terminal point are the same is called as the zero vector. Like the name suggests the magnitude of a zero vector is always equal to zero. The null vectors are written as PP, AA and so on.

Unit Vector: The magnitude of a vector when equal to 1 is called the unit vector.

Need an example? Here you go!

Find the magnitude of the vector AB given by (0, 1, 0).

Apply the formula for the magnitude of the vector. This is what you get:

math 2

Equal vector: Like the name suggests the equal vectors are the vectors which are the same in magnitude and direction. If AB and CD are two equal vectors, then they are given by AB = CD.

math 3

Negative Vector: Well again like the name suggests the vectors which have the same magnitude and are opposite in the direction are called the negative vectors. If OP is a vector than PO is called the negative vector. This can be represented as OP = – PO.

math 4

Here AB = – BA. So BA is the negative vector for vector AB.

Co-initial Vectors: Any given two vectors are called as co-initial vectors if both the given vectors have the same initial point. For example OA and OB are two co-initial vectors.

math 5

Collinear Vectors: Any two given vectors are called collinear vectors when both vectors are parallel to the same line.

math 6

In the above diagram AB and CD are parallel to the same line, hence the two vectors are collinear to each other.

Addition of vectors: Most students find it quite confusing to understand the addition of vectors. In simple terms here is how you can follow it:

math 7

In the above diagram E is the initial point for the vector EF and terminal point for vector DF. So to obtain the resultant we start from the initial point of one vector (DE) to the terminal point of another vector (EF). Hence the resultant of the vectors is DF.

                        This can be expressed as DF (resultant vector) = DE + EF.

Now that you are aware of the vector additions let us look at the properties of the vector space addition.

Commutative Property: Vector addition is commutative. Consider two vectors a and b, they can be expressed as: math 8 Associative property: Vector addition is also associative. Like associative property for numbers we need 3 vectors to express the associative property for vectors. The property can be written as follows: math 9 Scalar Multiplication: Now let us take a quick look at multiplying a vector by a scalar quantity. Let there be a scalar number or a constant k. Take a vector a. Now we can obtain a new vector by multiply with the constant k. This is expressed as ka, always remember that the vector obtained after the scalar multiplication is collinear to the given vector. So ka is collinear to vector a. The vector has positive of negative direction depending on the sign of k. Here are some examples to give better understanding: math 10 In the above diagram there is vector which is then multiplied with a scalar 2. Here 2 is a positive number so the direction of the vector 2a is the same but the magnitude of vector is twice the initial vector a. math 11 In the above diagram the vector is multiplied by the scalar number -3. Since the scalar is a negative number, the direction of the vector is the reverse to the direction of vector a. The magnitude of the vector will be thrice the magnitude of vector a. Do you now feel you have a better idea of the basics of the vector spaces? Well guess what this is just the beginning and there is lot more to learn and discover in linear algebra. So do not forget, keep practicing!

Free Online Math tutor is the easiest way to get solutions for difficult Math problems. Tutor Pace provides effective Math tutoring and assignment help which are personalized and customized to meet student demands in one to one sessions.