Working with physics concepts is not everyone’s cup of tea and especially when it comes to topics such as mirrors whether concave or convex, most students lack the understanding required to work with them. For instance, the mirror formula is quite difficult for most students and often they turn towards online physics tutors to get help with the topic. Read on to learn everything you need to know about the mirror formula and how it is derived.

Mirror Formula – what is it?

The mirror formula is essentially the relationship between an object (its distance), the image distance and the focal length. For a concave mirror, the formula goes as follows:

f – focal length, u – object distance, v – image distance

1/f = 1/u + 1/v

While we are at it, it is important to learn the sign conventions of spherical mirrors before we proceed with the derivation part.

How To Beat #Exam Blues With An Online #Physics Tutor https://t.co/hpsnH13mHR via @TutorPace

— Tutor Pace (@TutorPace) November 23, 2015

Sign Conventions and how they are used for Spherical Mirrors

There are three basic assumptions or conventions that one needs to know and they are:

• Every distance is measured from the pole of the mirror.
• Any distance that is measured in the direction of the ray of incidence or the incident ray is considered positive and the rays that are in the other direction (Opposite) are considered with a negative sign.
• Any distance that is measured above the principal axis is deemed positive and below is negative.

The below diagrams represent the conventions mentioned above for both the concave and the convex mirror.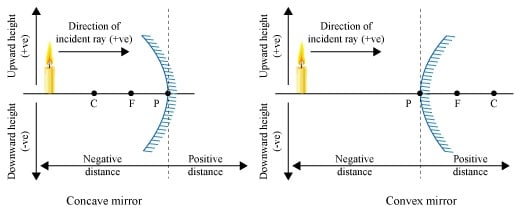

Derivation of the Mirror Formula for a Concave Mirror

This topic often sends students into a dizzy and assignments related to them are considered way too difficult. Learning the derivation properly can in itself serve as the best possible physics assignment help for students seeking to score straight A’s in their assignments. Read on to learn to derive the Mirror Formula.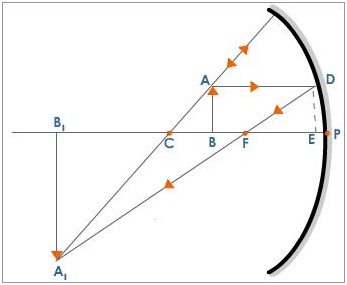

In the above figure, the object AB is at a distance ‘u’ from the pole of the mirror (marked by ‘P’ in the diagram). Its image is formed at A1B1, a distance of ‘v’ from the pole. In the above figures, angles A₁CB₁and ACB are vertically opposite and hence equal. Similarly, angles ABC and A₁B₁C are right angles and hence equal.

angle ACB = angle A₁CB₁

angle ABC = angle A₁B₁C = 90 degrees

Thus, the third angle B1A1C and BAC in the two triangles are equal too and thus these two triangles are similar.

As triangles A₁B₁C and ABC are similar, we can write the following:

AB/ A₁B₁ = BC/B₁C

In the same way, triangles, F B₁ A₁ and FED are similar. Thus, we can also write the following:

ED/ A₁B₁ = EF/F B₁

It is apparent from the figure that ED and AB are equal. Thus, the above two equations can be simplified as follows:

BC/B₁C = EF/F B₁

Assuming that D is very close to P and the distance between them is negligible, we can write the above equation as follows (assuming that EF = PF):

BC/B₁C = PF/F B₁

We now proceed to wrote BC, FB₁ and B₁C as follows:

BC = PC – PB

B₁C = PB₁ – PC

F B₁ = PB₁ – PF

Thus, the above equation can be rewritten as follows:

(PC-PB)/( PB₁ – PC) = PF/( PB₁ – PF)

PC = R, PB is u and PF is f. V here is represented by PB₁

The above equation thus further can be written as follows and with the sign convention, all of them take a negative sign which gives us:

(-R –(-u))/(-v –(-R)) = -f/(-v –(-f))

This gives us the following:

(-R + u) / (-v + R) = -f/(-v+f)

(u-R)/(R-v) = f/(v-f)

Cross multiplying and simplifying on both sides gives us the following:

uv – uf – Rv + Rf = Rf – vf

This further becomes:

uv – uf – Rv -= -vf

Since R = 2f, this can be written as:

uv – uf –2vf = -vf

This further gives us : uv – uf = vf

When you divide the above equation by uvf, you get the mirror formula:

1/f – 1/v = 1/u or alternately, 1/f = 1/u + 1/v.

Summary

Students usually look for physics homework help when it comes to understanding and working with concave and convex mirrors. Learning to derive the mirror formula will help students ace this topic and score high in physics tests.

I Passed My Exams With The Help Of Online Physics Tutor From Tutor Pace https://t.co/glgxgFiPAd via @TutorPace

— Tutor Pace (@TutorPace) November 23, 2015

Summary

Students usually look for physics homework help when it comes to understanding and working with concave and convex mirrors. Learning to derive the mirror formula will help students ace this topic and score high in physics tests.