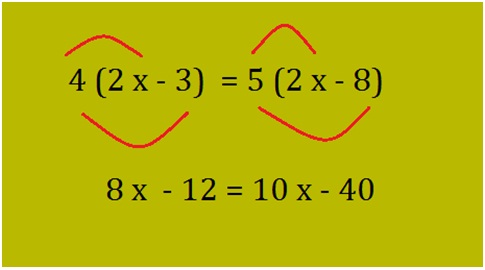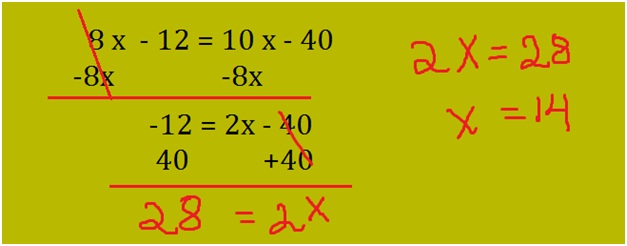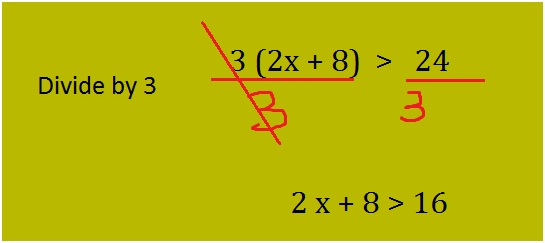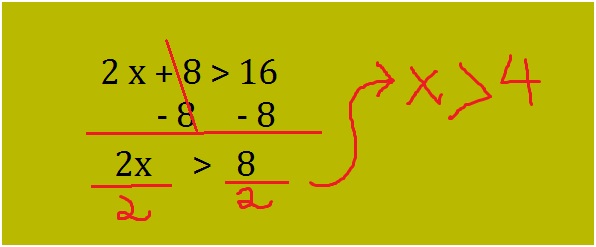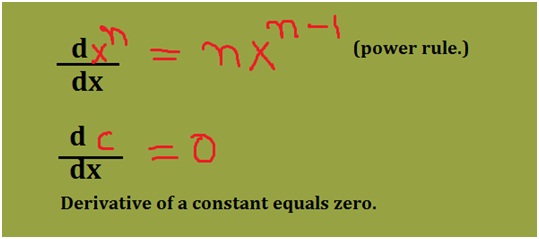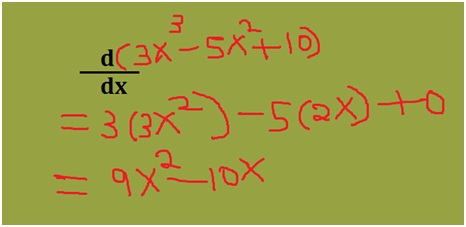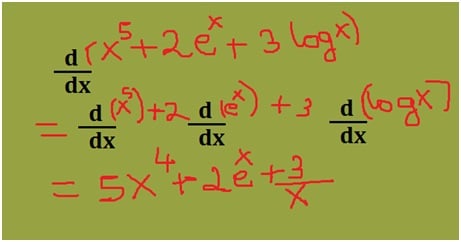Math is a combination of many branches such as Algebra, Geometry and Calculus, but math does not quite stop right there, we have levels to each branch of math such as beginners and advanced. The advanced level math usually needs more attention and practice to master it. If you are confident with the basics and know all your formulas then the advanced level math is the next step to beginner math topics. Today let us look at different advanced level math questions in areas such as Algebra, Geometry and Calculus.
5 Vedic #Math Secrets for Every Student to be a Math Genius http://t.co/MMgHewbMkX pic.twitter.com/RcUK3vAsmf
— Tutor Pace (@TutorPace) September 21, 2015
Advanced level Algebra
Algebra consists of different algebraic expressions and equations. Algebra has different kind of questions to solve. Mentioned below are few such questions which will give you an idea about how to use the basics of algebra to solve advanced level questions:
Solving linear equations with one variable:
Find the value for x in equation 4 (2x – 3) = 5 (2x – 8)?
Here the unknown variable is x. Since there are numbers in front of the brackets, distribute the numbers as shown below:
Here we have x on both sides of the equation, bring all like terms to the same side of the equation and solve for x.
As show above the equation reduces to 2x = 28. Divide by 2 on both sides of the given equation. This gives x = 14.
Did you follow the solution to the question above? Now let us look at solving an inequality. Solving inequities play an important role in algebra. An inequality is where there is a comparison and is represented by a less than or greater than symbol. The solution to the inequality are usually represented on a number line, so as to represent all the possible values for the variable. Follow the given example below:
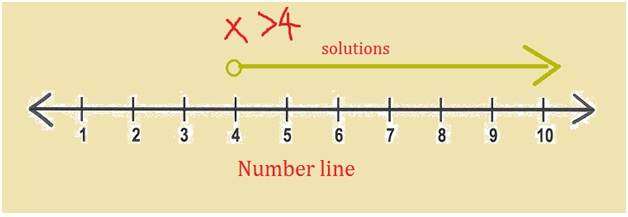
Solve the given inequality 3 (2 x + 8) > 24?
Look at the question we have greater than symbol here. You have to solve for the unknown variable x and find all the possible solutions for it. For the given question above, divide both sides of the equation by 3 as show below:
Now the inequality is reduced to the form 2x + 8 > 16. The next step is to solve for x. follow the steps below:
The inequality is now reduced to x > 4. Look at the symbol separating x and 4 it’s a greater than sign not greater than equal to. This implies that the number 4 is not included in the solution. Hence the solution of x contains all the values greater than 4 such as 5, 6, 7, 8…….. This can be represented on a number line as show below:
The advanced level algebra consists of many other subtopics such as quadratic equations, solving two variable equations using substitution and elimination methods and many more. The key to success for solving all such questions is practice and knowing the basics of Algebra.
Advanced level geometry:
After algebra let us look into geometry and some sample question. Geometry is one of the favorite topic for all the students especially when you are in the elementary school, it could be because of learning different kinds of shapes. But geometry does not quite stop there, as you go to the higher grades you need to tackle the advanced level. Let us look at two examples on how the basics of geometry can be helpful to solve the advanced level geometry question.
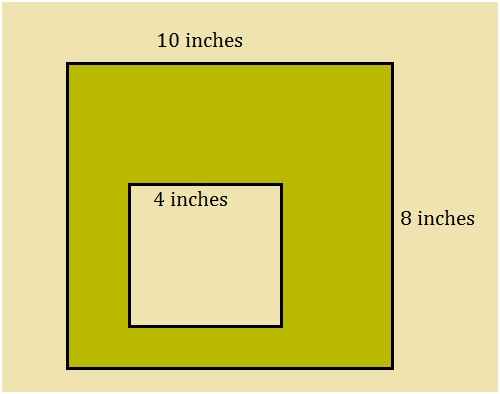
Find the area between the two shapes for the given geometric figure:
The given diagram is a square inscribed in a rectangle. Let us recall the formula for the area of the rectangle = length x width. Using the formula, the area of the rectangle = 10 x 8 = 80 square inches.
Now the area of the square = side x side. Using the formula, the area of the inner square = 4inches x 4inches = 16 square inches.
The area between the two geometric figures is obtained by the difference in the areas.
Hence, the area = (80 – 16) square inches = 64 square inches.
Did you follow the solution? Great! The next question you will see how the sum of the angles can be used to find the missing angles of the triangle.
The sum of all interior angles of a triangle = 180 degrees. This fact is very commonly used in solving many geometrical questions. Knowing the angle measures helps you classify the different kinds of triangles such as equilateral, scalene, and isosceles.
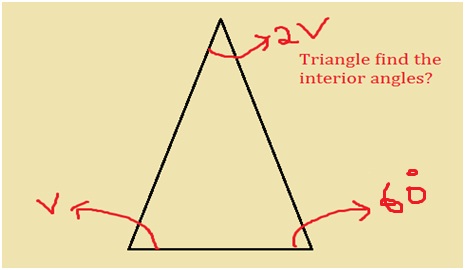
In the given diagram, find the value of v and the angles of the triangle. Classify the triangle?
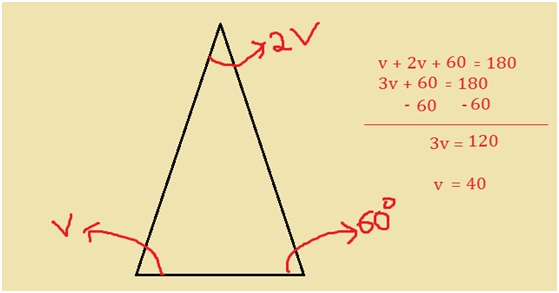
Sum of all the angles of a triangle = 180 degrees.
Adding all the angles of the triangle v + 2v + 60 = 180. This gives 3v + 60 = 180.
Solve for the variable v, follow the steps below:
The angles of the triangle are v = 40 degrees, 2v = 2 (40) = 80 degrees and the third angle is 60 degrees. Therefore, the angles of the triangle are 40, 60 and 80 degrees. Since all the angles of the triangle are different. The given triangle is a scalene triangle.
Advanced level Calculus
The next branch of mathematics which is very important and plays a major role in high school and college level math is calculus. The students are expected to know pre-calculus before stepping into calculus or advanced calculus. Calculus starts off form the basics of functions, domain, range and steps into differentiation and integration, which are the advanced level topics.
Let us take a quick look at few solved calculus questions:
Find the derivative to the function f (x) = 3x3 – 5x2 + 10?
Here before finding the derivative of the given question there are some formulas of derivatives which are expected to be known. Learn from the diagram below:
Did you recall the formulas? Now apply the power rule to 3x3 and -5x2. Since 10 is a constant the derivative will be zero. Take a look at the diagram below:
The answer f’(x) = 9x2-10x.
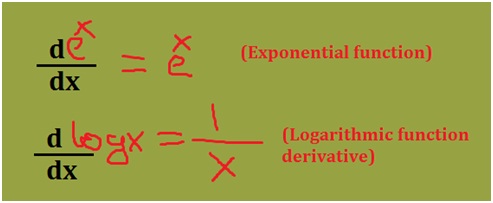
Taking a step forward, let us solve a derivative question involving logarithms and exponential functions.
Find the derivative of the function f(x) = x5 + 2ex + 3log x?
For the given question you can apply the power rule to x5, exponential rule for 2 ex and logarithmic rule for 3 log x. Use the formulas as mentioned in the diagram below:
Applying the formulas to the given function:
Hence the solution f’(x) = 5x4 + 2ex + 3/x.
How to Solve #Algebra Word Problems in 5 Steps http://t.co/kg6CqctO6O #backtoschool #homeschooling pic.twitter.com/wApx3S0D5R
— Tutor Pace (@TutorPace) August 4, 2015
Free Online Math tutor is the easiest way to get solutions for difficult Math problems. Tutor Pace provides effective Math tutoring and assignment help which are personalized and customized to meet student demands in one to one sessions.